Krótki przegląd:
  • Co to jest prostokąt?
  • Wzór na obliczenie pola prostokąta
  • Wzór na obliczenie pola prostokąta, gdy znany jest jeden bok i przekątna.
  • Wzór na obliczenie pola prostokąta, gdy znany jest obwód.
  • Jak rozpoznać prostokąt?
  • Czy prostokąt jest równoległobokiem?
  • Czy prostokąt jest trapezem równoramiennym?

Co to jest prostokąt?

Zgodnie z lekcją 13, Matematyka 8 (Tom 1) serii podręczników „Łączenie wiedzy z życiem” wydanej przez Vietnam Education Publishing House, prostokąt definiuje się jako czworokąt mający cztery kąty proste.

Właściwości prostokąta są takie, że ma dwa równoległe, przeciwległe boki, dwa równe, przeciwległe boki, dwa równe, przeciwległe kąty i dwie równe, przekątne, które przecinają się w środku każdej przekątnej.

pole prostokąta.png

Wzór na obliczenie pola prostokąta

W lekcji 52 podręcznika Math 3 (tom 2) z serii „Connecting Knowledge with Life” wydanej przez Vietnam Education Publishing House wzór na obliczenie pola prostokąta to długość pomnożona przez szerokość (stosując tę ​​samą jednostkę miary).

S = axb

Tam:

S: Pole prostokąta

a: Długość prostokąta

b: Szerokość prostokąta

Przykład: Prostokątny kawałek drewna ma szerokość 5 cm i długość 15 cm. Oblicz pole powierzchni tego kawałka drewna.

Odpowiedź: Pole powierzchni drewnianej deski wynosi: S = 5 x 15 = 75 ( cm² )

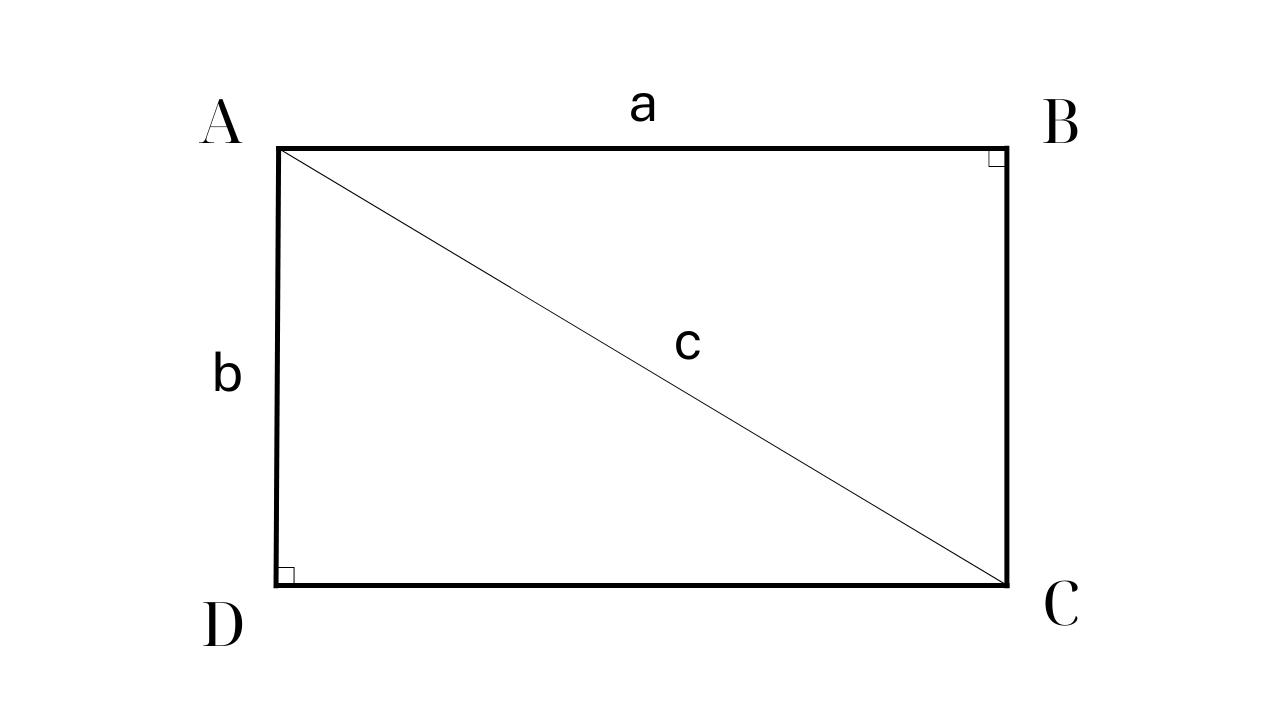
Wzór na obliczenie pola prostokąta, gdy znany jest jeden bok i przekątna.

Aby obliczyć pole prostokąta znając jego przekątną i jeden bok, należy połączyć twierdzenie Pitagorasa ze wzorem na pole powierzchni.

Krok 1: Zastosuj twierdzenie Pitagorasa do trójkąta prostokątnego, aby obliczyć długość pozostałego boku.

Krok 2: Zastosuj wzór na obliczenie pola prostokąta: S = axb

Przykład: Prostokąt ABCD ma AD = 60 cm i przekątną AC = 100 cm. Oblicz pole prostokąta ABCD.

Odpowiedź:

Krok 1: Znajdź pozostały bok prostokąta ABCD, korzystając z twierdzenia Pitagorasa w trójkącie prostokątnym.

Zatem: AC² = AB² + AD² => AB² = AC² - AD² = 10000 - 3600 = 6400 => AB = 80 (cm)

Krok 2: Pole prostokąta ABCD = AB x AD = 60 x 80 = 4800 ( cm² )

Wzór na obliczenie pola prostokąta, gdy znany jest obwód.

Aby obliczyć pole prostokąta, gdy znany jest obwód, należy połączyć wzór na obwód i wzór na pole podstawowe.

Krok 1: Ze wzoru na obliczenie obwodu prostokąta, który wynosi P = (a+b) x 2, gdzie P to obwód, a to długość, a b to szerokość prostokąta, otrzymujemy a = (P/2) - b lub b = (P/2) - a

Krok 2: Po znalezieniu a lub b zastosuj wzór na obliczenie pola prostokąta: S = axb

Jak rozpoznać prostokąt?

Zgodnie z Lekcją 13, Matematyka 8 (Tom 1) serii podręczników „Łączenie wiedzy z życiem” wydanej przez Vietnam Education Publishing House, charakterystycznymi cechami prostokąta są:

- Czworokąt ma 3 kąty proste (zgodnie z definicją)

- Równoległobok ma jeden kąt prosty.

- Równoległobok ma dwie równe przekątne.

- Trapez równoramienny ma kąt prosty.

Czy prostokąt jest równoległobokiem?

Zgodnie z Lekcją 13, Matematyka 8 (Tom 1) z serii podręczników „Łącząc wiedzę z życiem” wydanej przez Vietnam Education Publishing House, prostokąt ma wszystkie cechy równoległoboku. Dlatego prostokąt jest szczególnym rodzajem równoległoboku.

Czy prostokąt jest trapezem równoramiennym?

Lekcja 13, Matematyka 8 (Tom 1) – część serii podręczników „Łącząc wiedzę z życiem” wydanej przez Vietnam Education Publishing House – stwierdza, że ​​prostokąt posiada wszystkie właściwości trapezu równoramiennego. Dlatego prostokąt jest szczególnym rodzajem trapezu równoramiennego.

(Syntetyczny)

Źródło: https://vietnamnet.vn/cong-thuc-tinh-dien-tich-hinh-chu-nhat-2445253.html