Нещодавно багато експертів висловили різні думки щодо іспиту з математики та розподілу балів. Доктор Данг Куанг Вінь, дослідник штучного інтелекту (ШІ) та викладач кафедри комп'ютерних наук і технологій Британського університету В'єтнаму (BUV), також поділився цікавою пропозицією з точки зору ШІ з газетою Thanh Nien , сподіваючись, що Міністерство освіти та навчання найближчим часом змінить іспит з математики.
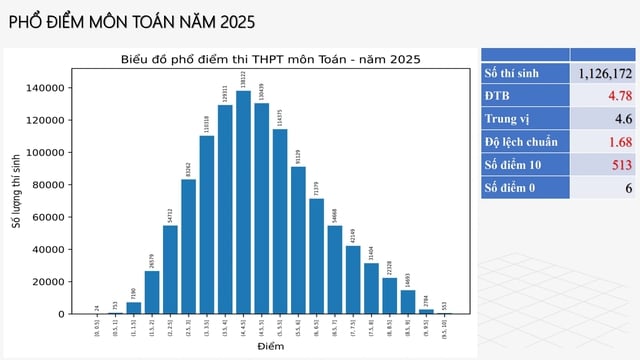
Розподіл балів з математики у 2025 році близький до нормального розподілу.
Однак, доктор Вінь також позитивно прокоментував розподіл балів на цьогорічному іспиті з математики. Розподіл балів на випускному іспиті з математики у середній школі був найближчим до нормального розподілу порівняно з розподілом балів з математики в останні роки. Це свідчить про високий ступінь диференціації на цьогорічному іспиті з математики.
Хоча розподіл балів виглядає нижчим, ніж минулого року, цьогорічний розподіл ближчий до концепції нормального розподілу в статистиці. Теоретично, саме цього ми можемо очікувати від стандартизованого іспиту, особливо коли він застосовується до великого набору даних, такого як кількість кандидатів, які складають іспит на випускний у середній школі. У таких випадках ідеальний розподіл балів повинен наближатися до нормального розподілу. Тому можна оцінити, що цьогорічний розподіл балів є прийнятним.
Нижчий середній бал насправді є позитивним знаком для освіти . Якщо іспит занадто легкий і багато кандидатів отримують ідеальні бали, іспит втратить свою функцію класифікації та оцінки справжніх здібностей.
Д-р Вінх сказав: «Ми всі розуміємо, що бали відображають здібності лише відносною мірою, але значна різниця, така як між балом 8 та балом 3, все ще відображає нерівність у підготовці та навчальному настрої. Крім того, якщо забагато студентів досягають ідеальних балів, це свідчить про те, що іспит був недостатньо складним, щоб повною мірою розкрити їхні здібності. Це вказує на те, що деякі студенти могли б отримати вищі бали – 11, 12 або навіть 15 балів, якби шкала оцінювання дозволяла».
Таким чином, більш рівномірний розподіл балів, без концентрації високих балів, допомагає нам краще класифікувати кандидатів і дозволяє їм повною мірою продемонструвати свої здібності. Це позитивний аспект цьогорічного іспиту з математики та розподілу балів.
Запитання не повинні бути розроблені таким чином, щоб вимагати від кандидатів лише вибору відповіді.
Однак, за словами доктора Вінха, з точки зору штучного інтелекту, той факт, що математичні питання повністю мають формат множинного вибору, як-от нинішній випускний іспит у середній школі, не відповідає цілям математичної освіти.
В останні роки багато хто хвилюється, що ШІ може надавати відповіді дуже швидко, але не може пояснити, чому він так думає. Це робить ШІ ненадійним у галузях, що вимагають ретельного мислення. Тому сучасна тенденція розвитку полягає в інтеграції можливостей мислення в ШІ, щоб він не лише отримував правильні результати, але й пояснював процес отримання цих висновків.
І це показує, що здатність до міркування є унікальною перевагою людей, аж до того, що штучний інтелект також прагне її досягти.
«Тому немає жодної причини відмовлятися від цієї переваги. Навпаки, освіта повинна заохочувати та розвивати навички міркування, особливо за допомогою іспитів на основі есе», – сказав доктор Вінх.
За словами доктора Вінха, протягом усієї історії математики ми бачили, що процес міркування часто дає більшу цінність, ніж кінцевий результат. Зосередження виключно на відповіді, ігноруючи процес міркування, суперечить духу математичного мислення.
З огляду на нинішні темпи розвитку, штучний інтелект, безсумнівно, перевершить людей у своїй здатності давати результати, особливо в суто обчислювальних завданнях або отриманні історичних даних. Однак, штучний інтелект не може замінити людей в інтерпретації та представленні процесів логічного мислення, принаймні наразі.
Д-р Вінь поділився: «Я повністю підтримую розробку екзаменаційних питань на основі есе для оцінки здібностей студентів до міркування та логічного мислення. Саме такий підхід ми застосовуємо в BUV».
На багатьох шкільних іспитах, навіть на факультеті комп'ютерних наук та технологій, галузі, яка може здатися зосередженою виключно на сухих розрахунках, студенти повинні не лише давати відповіді, а й пояснювати свої міркування, або за допомогою письмових завдань, або презентацій у класі. Нікому не дозволено запитувати щось на кшталт «Скільки буде 1 + 1?», і просто писати «2».
Джерело: https://thanhnien.vn/thay-doi-de-thi-toan-the-nao-trong-thoi-dai-ai-185250719210628563.htm
Коментар (0)