Les élèves apprennent-ils les « mathématiques sans réfléchir » ?

Existe-t-il une forme de mathématiques « sans réflexion » ?

Le Dr Nguyen Phi Le (Faculté des technologies de l'information et de la communication, Université des sciences et technologies de Hanoï ) était autrefois un excellent élève en mathématiques, remportant une médaille d'argent aux Olympiades internationales de mathématiques (OIM) de 2000 sans avoir besoin de suivre beaucoup de cours particuliers. Par conséquent, lorsque son enfant était encore à l'école primaire, le Dr Le ne jugeait pas nécessaire qu'il prenne des cours de mathématiques supplémentaires en général, et encore moins des cours de « raisonnement mathématique » en particulier, même si de nombreux centres de soutien scolaire commençaient à proposer ce type d'enseignement. Cependant, lorsque son enfant est entré en CM2, puis a passé le concours d'entrée en seconde, le Dr Le a été contraint de l'inscrire à des cours de mathématiques supplémentaires, car c'était la seule façon pour lui de réussir le concours d'entrée dans les écoles spécialisées et les classes sélectives.

Nombreux sont les parents qui initient leurs enfants aux mathématiques dès leur plus jeune âge, dans l'espoir que ces derniers réussissent bien dans cette matière.

Par exemple, récemment, après l'examen d'entrée en seconde spécialisée en mathématiques au lycée des sciences naturelles de l'université des sciences naturelles de Hanoï, professeurs et élèves ont longuement discuté d'un problème de géométrie. Un professeur de géométrie expérimenté a confié avoir passé trois à quatre heures à résoudre ce problème. Or, un élève de troisième devait le faire en un temps très court. Dans ce cas précis, un élève n'ayant pas fait d'examens blancs et n'ayant jamais travaillé sur des problèmes similaires était voué à l'échec. Même un élève doté d'excellentes capacités de raisonnement n'y parviendrait pas.

« Il faut faire passer un test très difficile, avec un format inhabituel, en un temps très court. Pour réussir un tel test, les étudiants ont besoin de beaucoup de temps », a expliqué le Dr Le.

Le Dr Le a également raconté que, voyant son enfant suivre trop de cours particuliers, elle lui avait conseillé de consacrer plus de temps à l'étude personnelle. Selon elle, c'est la seule façon pour son cerveau d'assimiler les connaissances, de développer son autonomie et de se débrouiller seul face aux problèmes. Cependant, son enfant n'était pas rassuré, car il craignait de ne pas pouvoir rivaliser avec ses camarades, dont la force résidait dans les cours préparatoires aux examens.

Selon le professeur Le Anh Vinh, directeur de l'Institut vietnamien des sciences de l'éducation , de nombreux mathématiciens sont réticents à l'idée d'apprendre à « penser en mathématiques ». Car, selon eux, cela sous-entendrait l'existence de « mathématiques sans réflexion ». Or, la réalité est que les méthodes d'enseignement actuelles privilégient souvent l'apprentissage du calcul plutôt que la réflexion. En classe, les enseignants se contentent généralement de faire résoudre aux élèves des exercices à partir de modèles (ce qu'on appelle souvent les mathématiques formelles). Avec cette méthode, lorsqu'ils sont confrontés à un problème mathématique donné, les élèves le résolvent souvent très rapidement, sans réfléchir.

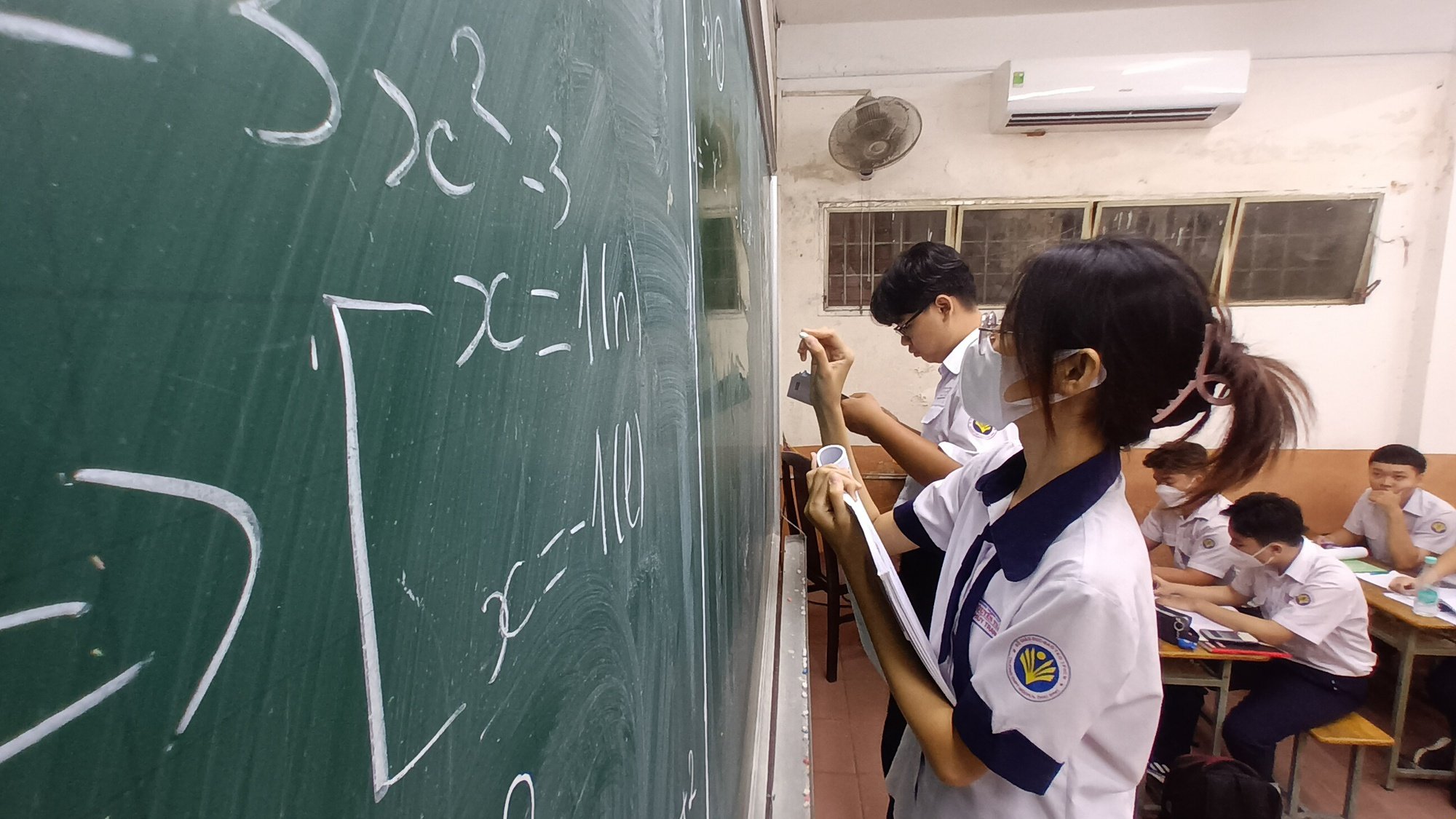
Le nouveau programme d'enseignement général met l'accent sur les mathématiques liées à la pratique, à l'application, à la résolution de la question « à quoi servent les mathématiques ? », et non pas seulement sur la réalisation d'exercices.

QUAND L'APPRENTISSAGE DES MATHÉMATIQUES N'EST PLUS LA NATURE DE L'APPRENTISSAGE DES MATHÉMATIQUES

Selon le Dr Vu Thi Ngoc Ha, de l'Institut de mathématiques appliquées et d'informatique de l'Université des sciences et technologies de Hanoï, chaque discipline scientifique favorise le développement et le perfectionnement de la pensée chez chaque enfant, ce qu'on appelle la « diversité des domaines fondamentaux », et non pas seulement l'apprentissage des mathématiques qui développe la pensée.

En mathématiques, les problèmes sont toujours ancrés dans la réalité. Pour réussir, l'enfant doit procéder par étapes : construire le problème en analysant les lois des phénomènes naturels, puis utiliser la pensée logique et créative pour le résoudre. Ce processus stimule parfois l'imagination et l'esprit critique.

« Les mathématiques semblent être la discipline qui stimule le plus la pensée la plus aboutie. Dès lors, la création de centres de « pensée mathématique » se comprend aisément, compte tenu de l'obligation actuelle de maîtriser un module de connaissances précis dans chaque matière, et pas seulement en mathématiques, dans un délai très court, en vue des examens. Dès lors, l'apprentissage des mathématiques ne correspond plus à sa véritable nature », a commenté le Dr Ngoc Ha.

Le professeur Le Anh Vinh a confié qu'au départ, il était lui aussi réticent à l'expression « mathématiques réflexives ». Après des recherches ultérieures, il s'est avéré que l'enseignement des mathématiques sans réflexion restait assez répandu. Le professeur Vinh a commenté : « Dire que nous enseignons les mathématiques ici, et non pas les mathématiques sans réflexion, sonne trop lourd. Par conséquent, lorsqu'une personne ou un organisme se présente comme enseignant les mathématiques réflexives, cela signifie qu'il s'agit d'enseigner les mathématiques au sens propre du terme. Ainsi, l'expression « mathématiques réflexives » vient du fait que l'on souhaite enseigner les mathématiques de manière à ce que les élèves réfléchissent et soient capables de les appliquer dans la vie courante, et non pas de façon mécanique, dans le seul but d'obtenir d'excellentes notes aux examens. Les parents devraient également y réfléchir, car se présenter ainsi signifie non pas enseigner les mathématiques à leurs enfants pour réussir des tests, mais leur apprendre à penser. »

NÉCESSAIRE À L'INNOVATION DANS L'ÉVALUATION

Le Dr Ngoc Ha estime que pour que l'apprentissage des mathématiques retrouve sa véritable nature, les élèves doivent « apprendre lentement », car « l'apprentissage lent » est le moyen le plus efficace de stimuler le développement de la pensée de chaque enfant.

Face à un problème, les élèves doivent disposer de beaucoup de temps pour identifier les phénomènes naturels, puis rechercher les quantités et les règles permettant d'établir des relations entre ces quantités par le biais d'expressions, et enfin trouver les outils méthodologiques nécessaires à la résolution du problème. De ce fait, concevoir un programme intitulé « penser les mathématiques » est une tâche complexe. Mais l'enseignement l'est encore plus, car outre une progression très lente, l'enseignant doit posséder de solides connaissances générales. L'enseignement doit être flexible et adapté aux qualités et aux aptitudes de chaque élève. Or, cela s'avère très difficile sous la pression de la réussite scolaire, avec les prix, les notes et les attentes des parents, qui pèsent sur le temps libre de l'enfant…

Apprenez aux élèves à penser, pas à calculer.

Le professeur Le Anh Vinh dit souvent en plaisantant aux professeurs de mathématiques : apprendre aux élèves à réfléchir pendant dix minutes est plus difficile que de leur apprendre à calculer pendant une heure. Si aller à l’école se résume à recevoir une feuille d’exercices et à calculer le plus rapidement et le plus efficacement possible, alors à la fin du cours, les élèves n’auront plus rien retenu. Face à des situations nouvelles, ils seront incapables de réfléchir, d’appliquer leurs connaissances pour résoudre des problèmes. Or, ce problème est systémique : les examens, les contrôles et les exercices en général font l’impasse sur tout ce qui développe la pensée, au profit d’un enseignement axé uniquement sur le calcul et la réalisation d’exercices.

En particulier, enseigner les mathématiques comme un enseignement de la pensée exige la synchronisation de tout un système : programme, manuels, gestion du temps (à chaque heure et à chaque minute), chaque matière, système d’évaluation, psychologie sociale…

Des élèves de 3e (9th grade) à Hô Chi Minh-Ville passent l'examen de mathématiques d'entrée en seconde (10th grade). L'épreuve comportait de nombreux problèmes pratiques.

Selon le professeur Vinh, le nouveau programme d'enseignement général met l'accent sur le lien entre les mathématiques et la réalité, leur application et la résolution de la question du pourquoi nous apprenons les mathématiques, et non pas seulement sur la réalisation d'exercices.

La docteure Phi Le a déclaré qu'elle soutenait la possibilité pour les élèves de suivre des cours supplémentaires dans des matières qui les intéressent et dans lesquelles ils sont compétents, à condition que ces cours stimulent leur créativité et leur capacité de réflexion. Les cours supplémentaires axés sur la préparation aux examens, tels qu'ils sont actuellement pratiqués, ne sont pas très bénéfiques pour les élèves. « Le problème, c'est que la formulation actuelle des questions désavantage les élèves qui n'ont jamais étudié les types de questions posées à l'examen. Le contexte actuel des examens crée une concurrence inégale entre les élèves qui apprennent à réfléchir et ceux qui apprennent à se préparer aux examens. Réfléchir demande beaucoup de temps et implique d'accepter le risque de ne pas connaître tous les types de questions. C'est cette motivation qui pousse les élèves à suivre des cours supplémentaires. »

« Comment concevoir des examens qui développent la pensée critique des élèves ? ​​Les questions ne doivent pas être piégeuses, doivent être cohérentes avec le contenu enseigné dans les écoles générales et doivent également permettre de déceler les élèves dotés d’un bon esprit critique », a déclaré le Dr Phi Le.

Lien source: https://thanhnien.vn/phai-chang-hoc-sinh-dang-hoc-toan-khong-tu-duy-185230609045433219.htm