Problem ze znalezieniem kota za drzwiami

Zadanie matematyczne dla klasy 5 polega na obliczeniu liczby drzwi, które należy otworzyć, aby znaleźć kota, wiedząc, że po każdym otwarciu pustych drzwi kot przejdzie do innych drzwi.

Temat:

Prosty korytarz ma po jednej stronie pięcioro drzwi. Za jednymi z nich kryje się kot. Twoim zadaniem jest znalezienie kota poprzez otwarcie odpowiednich drzwi. Możesz otworzyć tylko jedne drzwi dziennie. Jeśli kot tam jest, wygrywasz.

Jeśli kota nie ma, drzwi się zamkną i będziesz musiał poczekać do następnego dnia, zanim będziesz mógł je ponownie otworzyć. Kot ciągle się porusza i każdej nocy przenosi się za inne drzwi. Drzwi, do których się przesunie, będą drzwiami po lewej lub prawej stronie od miejsca, w którym aktualnie się znajduje.

Ile dni potrzebujesz, żeby mieć pewność, że znajdziesz kota?

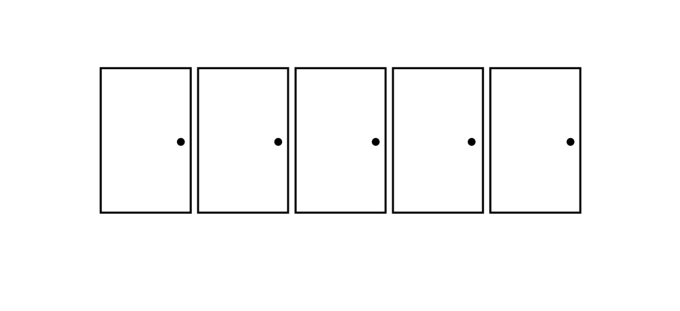
Zadanie polega na znalezieniu strategii gwarantującej złapanie kota w ciągu określonej liczby dni, niezależnie od tego, za którymi drzwiami zacznie i dokąd przejdzie w nocy. Kluczem do rozwiązania problemu jest rozpoczęcie od mniejszej liczby drzwi, znalezienie schematu, a następnie zwiększenie ich liczby.

Zacznijmy od przypadku, gdy są tylko trzy drzwi. Jeśli otworzysz środkowe drzwi dwa dni z rzędu, masz gwarancję, że złapiesz kota, ponieważ jeśli kot nie jest za środkowymi drzwiami pierwszego dnia, musi być za jednymi z dwóch skrajnych. A jeśli jest za jednymi z skrajnych drzwi pierwszego dnia, nie ma innego wyboru, jak tylko przejść do środkowych drzwi drugiego dnia.

Jeśli jest czworo drzwi, możesz złapać kota w cztery dni. Wyjaśnienie znajdziesz w odpowiedzi poniżej, ale zanim to zrobisz, spróbuj wyjaśnić to sam. Pamiętaj, że kot porusza się tylko do drzwi znajdujących się bezpośrednio po jego prawej lub lewej stronie i może wrócić do drzwi, za którymi wcześniej stał. Wierz, że poczujesz się szczęśliwy, gdy znajdziesz wyjaśnienie.

>>>Odpowiedź

Vo Quoc Ba Can

Nauczyciel matematyki, Szkoła Archimedesa w Hanoi

Link źródłowy: https://vnexpress.net/bai-toan-tim-con-meo-sau-canh-cua-4604654.html